a typical synthesis problem

As Leslie puts it, you must define the problem first before solving it. This post is about how to define and analyze a typical synthesis problem, along with a naive solution.

grass turtle and mushrooms

Imagine you’re building a rectangular turtle enclosure on a field of 6x6 grid. You want to keep the grass inside the enclosure, and keep the mushrooms outside.

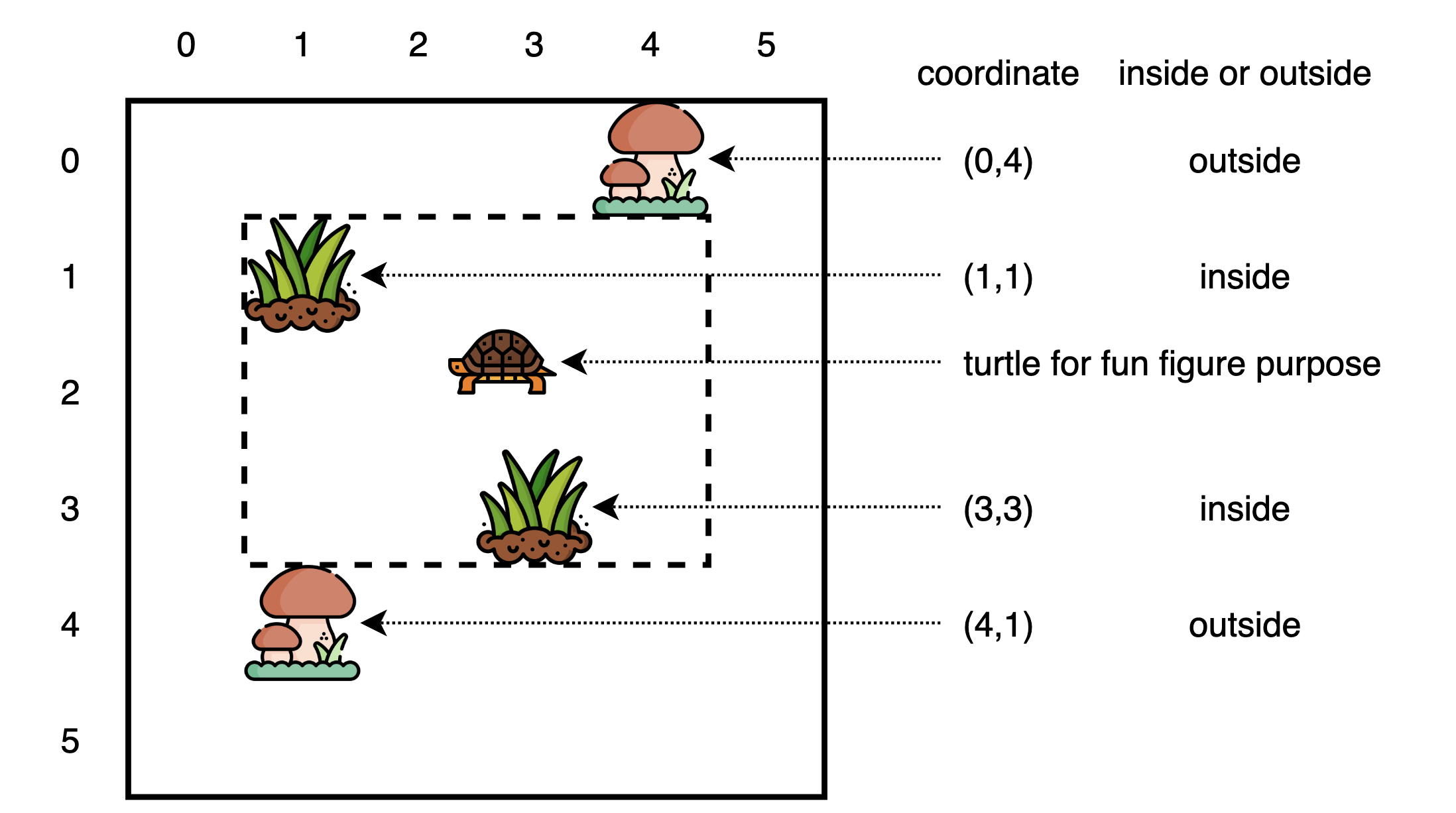
Given a field, how do you quickly come up with a working rectangle?

modeling programming

Program synthesis starts with programming. Programming starts with an interpreter.

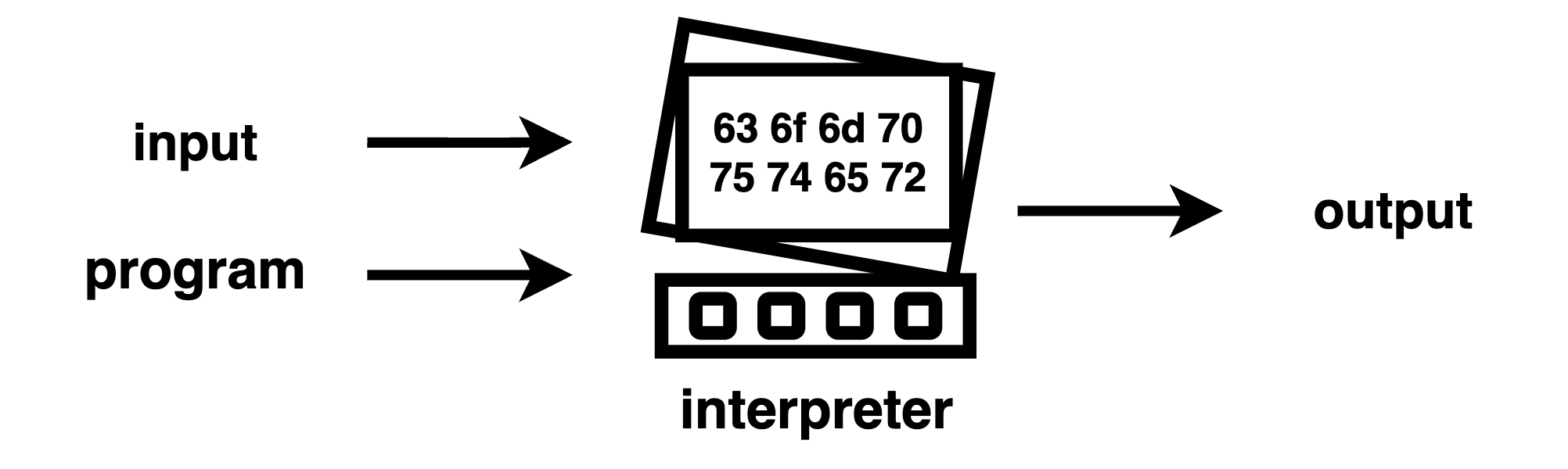
Here’s how to model an interpreter for our task.

program

The program is a data-structure. Here, a program is a rectangle, defined by top, down, left, right.

# the rectangle in our figure, [T,D,L,R]
rectangle = [1,3,1,4]

input

The input is a data-structure. Here, the input is a coordinate, defined by (row, col).

# the mushrooms and grass coordinates in our figure
shroom1 = (0,4)
shroom2 = (4,1)
grass1 = (1,1)
grass2 = (3,3)

output

The output is a data-structure. In our case, it simply indicates inside or outside

inside = True
outside = False

interpreter

The interpreter is a function (program, input) → output. In our case, given a program (a rectangle, i.e. [1,3,1,4]) and an input (a coordinate, i.e. (3,3)), our interpreter interprets, or executes the program on the input by returning if the coordinate is inside or outside the rectangle.

def interpret(program, inputt):
    T, D, L, R = program
    i, j = inputt
    return i >= T and i <= D and j >= L and j <= R

The interpreter gives semantics to a program – without the interpreter, the program is but a lifeless pile of syntax ([1,3,1,4] isn’t a rectangle on its own).

putting it together

Does our rectangle include the grass, and exclude the mushrooms?

assert interpret(rectangle, grass1) == inside
assert interpret(rectangle, grass2) == inside
assert interpret(rectangle, shroom1) == outside
assert interpret(rectangle, shroom2) == outside
print ("working as intended !")

programming

How does a programmer write a program, so that the interpreter does the right thing for a task?

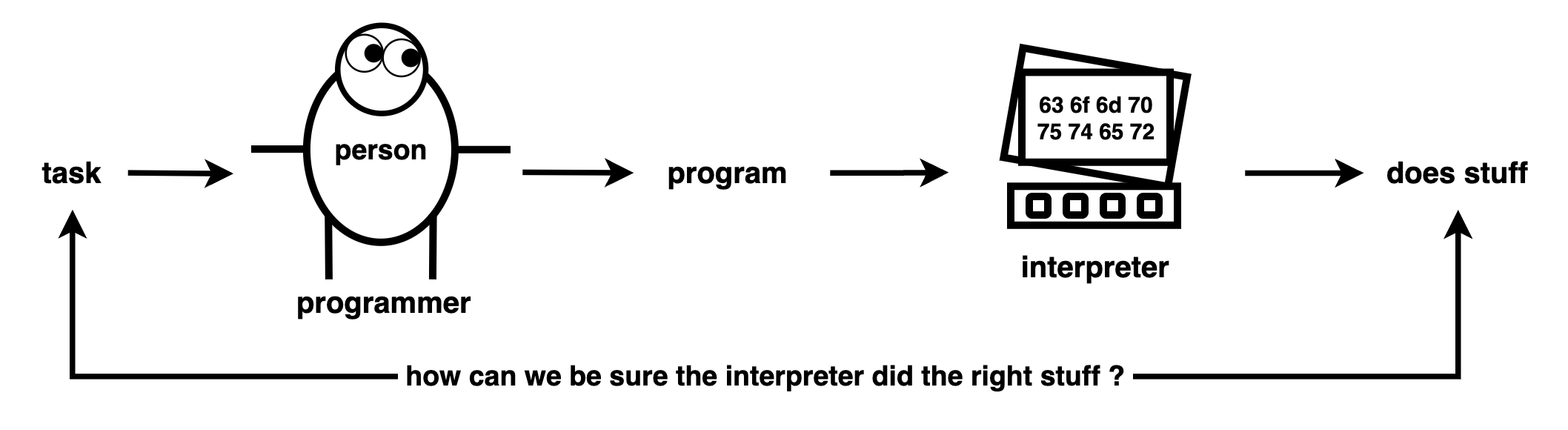
There are many ways to specify a task – imagine the different ways you can ask a developer to build an App. There are many ways to check if a program is “correct” – imagine the different ways to test the App they built. People’s real-life tasks can rarely be understood by computers.

task as specifications

A specification or spec is a way of stating the task so that both human and computer can agree on what needs to be done. In program synthesis, a spec is typically given as a list of input-outputs. Input-output is one of the rare, special form of communication that is readily understood by both humans and computers.

There are other forms of specifications, for instance, it could be an objective function¹ to be maximized, a set of constraints on the computer’s behaviours², or a natural language sentence³. I hope to cover these topics at a different time!

Here are some specs.

spec = [(grass1, inside), (grass2, inside), (shroom1, outside), (shroom2, outside)]
shroom3 = (2,2)
grass3 = (4,3)
shroom4 = (5,4)
spec2 = [(shroom3, outside), (grass3, inside), (shroom4, outside)]

correctness

With a spec, the computer can automatically decide if a program “did the right stuff” by checking if executing the program on the inputs produces the corresponding outputs.

def is_correct(program, spec):
    for inputt, output in spec:
        if interpret(program, inputt) != output:
            return False
    return True

programming problem

A typical programming problem consists of a human writing both the specification and the program, and having the computer to check if the program meets the specification.

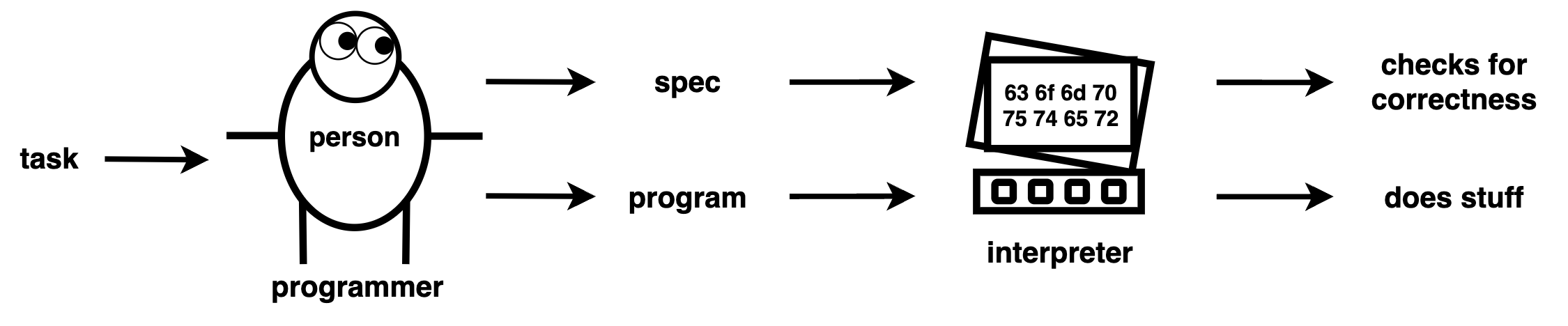
It is crucial to solve a few programming problems by hand before attempting program synthesis. It gives insights on how to build a machine synthesizer capable of doing the same.

# let's try to make a rectangle that satisfy spec2
rect2 = [1,3,1,4]
print (is_correct(rectangle, spec2)) # didn't work
rect3 = [3,4,1,3]
print (is_correct(rect3, spec2)) # worked okay

Our programming environment, rectangle.py can be found here.

the asymmetry

It is often easier to write the specification than it is to program. This asymmetry alone motivates program synthesis. Do not attempt program synthesis if this asymmetry is not present⁴.

Let’s take a break. no seriously follow along and rest your eyes.

a typical synthesis problem

With the synthesizer, a programmer writes the specification (a form of easier programming), and leaves the harder programming to the synthesizer.

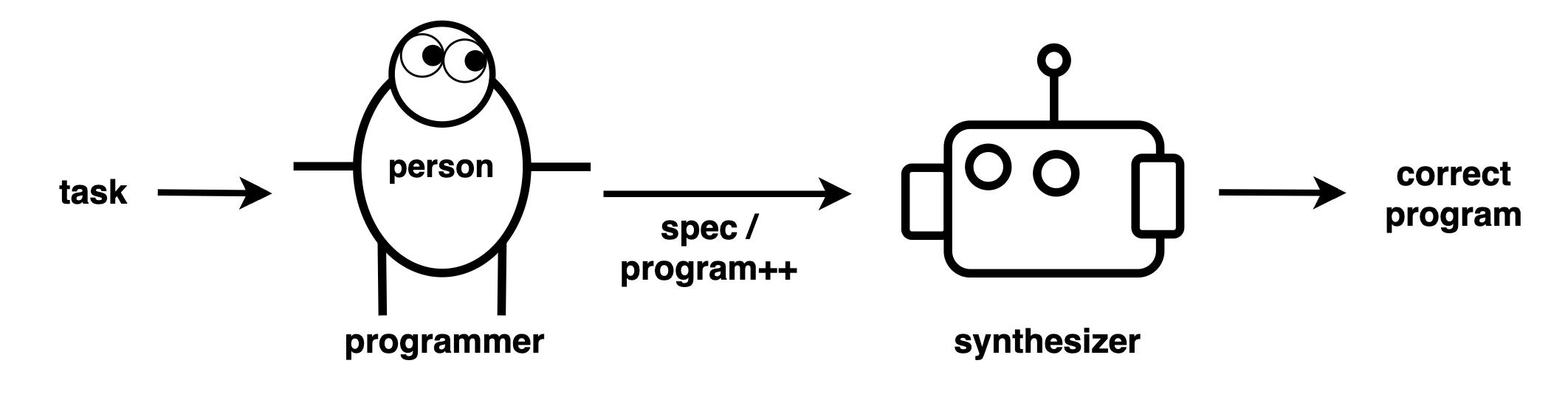
The synthesis problem is turning specs into programs. It is formalized using the meaning matrix.

characterize the synthesis problem with meaning matrix M

Imagine you have infinite computation, and construct the meaning matrix M M = spec x prog. Each row is a specification, each col is a program, and each entry relates the two using the interpreter – M[spec,prog] = is_correct(prog,spec).

M completely characterizes the synthesis problem. Assuming M can be built, the synthesis problem becomes trivial: Given a spec (row), look up a prog (col) such that the matrix entry M[spec,prog] = True.

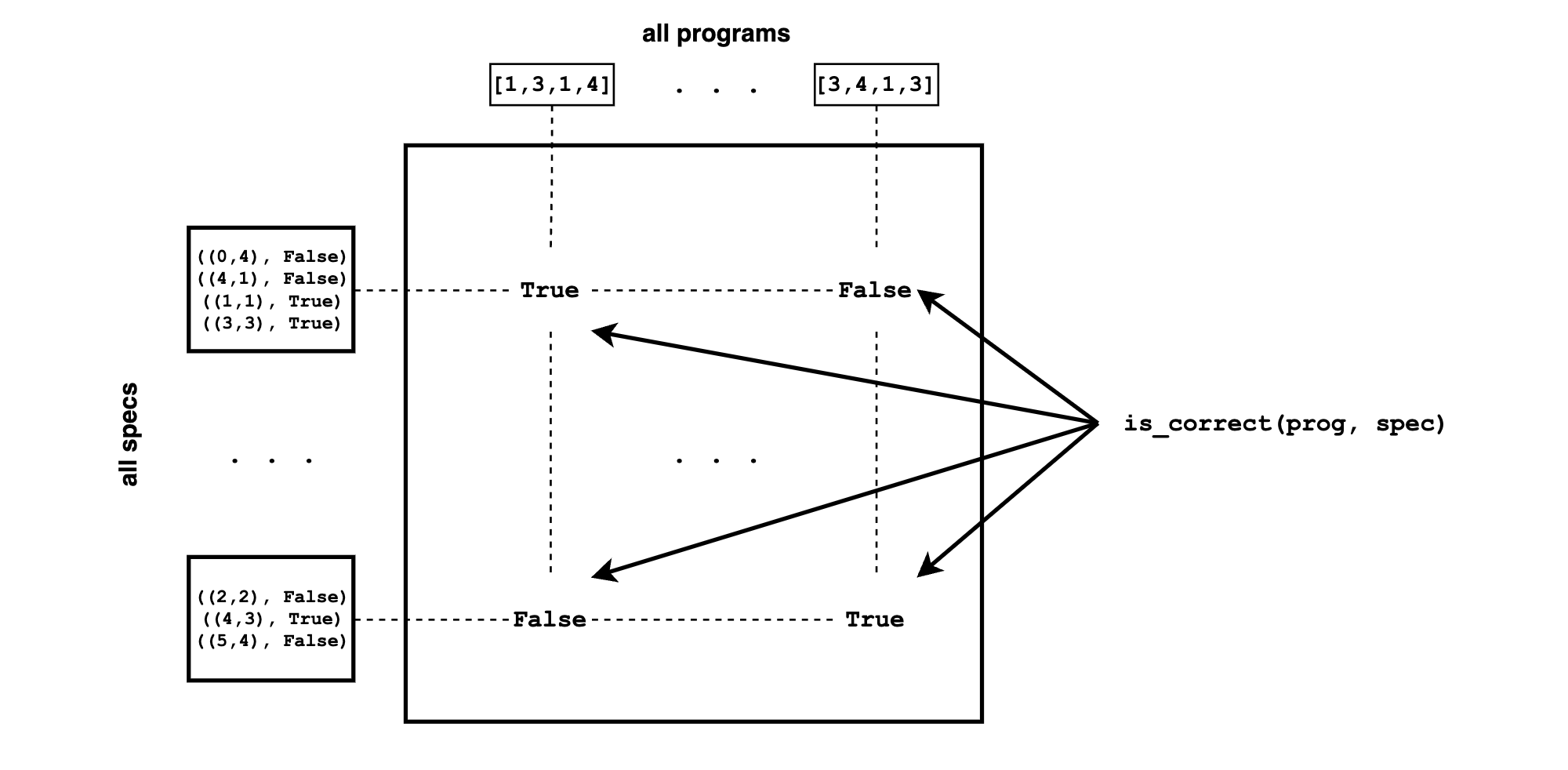
using M to quantify difficulty

How difficult is our synthesis problem? Some quick maffs : Number of programs/rectangles is roughly 6^4, inputs/coordinates is 6^2, outputs/booleans is 2. There are (6^2)*2 input-output pairs. Assuming up to 10 grass and mushrooms on the field, there are roughly ((6^2)*2)^10 specs. Thus, we need to pre-compute a matrix of ((6^2)*2)^10 x 6^4 = 4.852e+21. Oh no.

Synthesis starts with writing down M – the horrific combinatorial monster. Understanding and approximating the structure of M is how we fight the monster with limited computations.

a typical synthesis algorithm

Rather than pre-computing the entirety of M, a typical program synthesis algorithm samples elements from a specific row M[spec,:]⁵. This algorithm has a program writer that proposes different programs based on tasks, and a program checker that uses the interpreter and the specification to check if the proposed programs are correct.

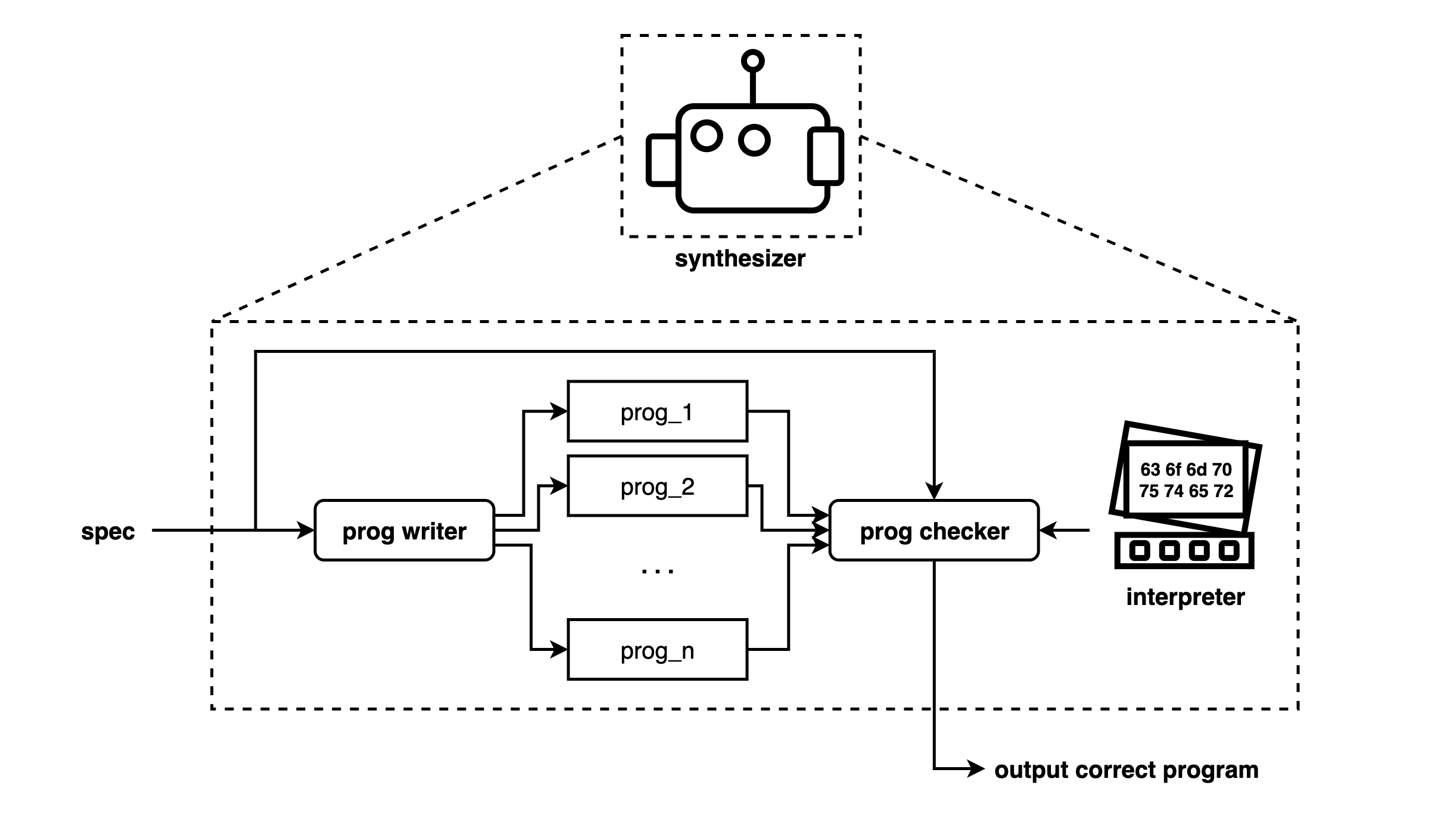
program writer

The writer proposes programs given specs. Consider the most naive program writer that simply writes a random program.

def random_writer(spec):
    # ignores the spec, W=6 globally
    T, D, L, R = random.randint(0,W), random.randint(0,W), random.randint(0,W), random.randint(0,W)
    return [T, D, L, R]

program checker

The is_correct function we wrote is the checker we need – it internally uses the interpreter.

def program_cheker(prog, spec):
    return is_correct(prog, spec)

putting it together

We will use budget to denote how many programs our writer can propose before giving up.

# a synthesizer that returns both a working program (if it finds any)
# and the number of samples it took to find it
def get_synthesizer(writer, checker, budget):
    def synthesizer(spec):
        prog = writer(spec)
        for i in range(budget):
            prog = writer(spec)
            if checker(prog, spec):
                return (i, prog)
        return None
    return synthesizer

Let’s try it!

synthesizer = get_synthesizer(random_writer, program_cheker, 1000)
spec1 = [( (0,4), outside), ( (4,1), outside), ( (1,1), inside), ( (3,3), inside)]
n_tries, prog = synthesizer(spec1)
print (n_tries, prog) 
# results vary, but I got 146 [1, 3, 0, 3], 31 [1, 3, 0, 5], 56 [1, 3, 1, 6], etc

It is not terribly efficient.

making the writer better

Instead of ignoring the spec, maybe it is a good idea to only use the coordinates of the grass (inside) as the parameters of the rectangle.

def better_writer(spec):
    # get the coordinates of spec that are inside
    inside_coords = [coord for coord,bool in spec if bool]
    if inside_coords == []:
        # if there are no inside coordinates, default to a random
        return random_writer(spec)
    # otherwise, use the inside coords to suggest parameters of the rectangle
    row_coords = [coord[0] for coord in inside_coords]
    col_coords = [coord[1] for coord in inside_coords]
    T, D = random.choice(row_coords), random.choice(row_coords)
    L, R = random.choice(col_coords), random.choice(col_coords)
    return [T, D, L, R]

Let’s try it!

synthesizer2 = get_synthesizer(better_writer, program_cheker, 1000)
n_tries, prog = synthesizer2(spec1)
print (n_tries, prog)
# results vary, but I got 1 [1, 3, 1, 3], 23 [1, 3, 1, 3], 5 [1, 3, 1, 3], etc

This is much better than using the random writer on first glance.

exercise

reading exercise

Read the following papers, pay more attention to their synthesis problem statement, and less to how they solve the synthesis problem. robustfill, execution guided synthesis, repl, deepcoder, language to prog, csg-net, shrdlurn. For each paper, conceptualize the meaning matrix M – specifically, answer the following questions:

• what is the DSL or space of programs considered? how big is the space (i.e. 1e4 or 1e20)?
• how are the programs executed on the interpreter?
• what is the space of specifications? how big is this space? is the specification given as input-output / logical constraints / natural language ?
• what is the is_correct criteria for this domain?
  • is there even a way for the computer to automatically check if a program is correct given a specification?
  • is this is_correct check cheap or expensive to perform?

coding exercise

How do the writers compare on a variety of different specs? Can you come up with a even better program writer? Explore these questions by using the synthesizer code here.

– evan 2022-08-12

up next

The next post cover how to systematically generate programs with language models. let’s go for it

notes